What are Option Greeks?

Option Greeks are important financial measures that determine the sensitivity of an option's price to its underlying determining parameters, such as volatility or the price of the underlying asset. They are utilized to analyze an option's portfolio and conduct sensitivity analyses of options or portfolios of options. Many investors consider these measures essential for making informed decisions in options trading.
The key option Greeks are Delta, Gamma, Vega, Theta, and Rho. However, many other option Greeks can be derived from those mentioned above. These Greeks are as follows:
Delta
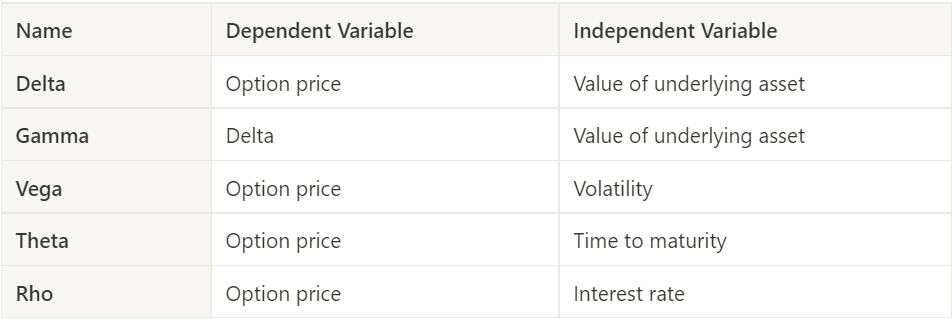
Delta (Δ) is a measure of the sensitivity of an option’s price changes relative to the changes in the underlying asset’s price. In other words, if the price of the underlying asset increases by $1, the price of the option will change by Δ amount. Mathematically, the delta is found by:
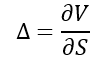
Where:
- ∂ – the first derivative
- V – the option’s price (theoretical value)
- S – the underlying asset’s price
Keep in mind that we take the first derivative of the option and underlying asset prices because the derivative is a measure of the rate change of the variable at a given period.
The delta is usually calculated as a decimal number from -1 to 1. Call options can have a delta from 0 to 1, while put options have a delta from -1 to 0. The closer the option’s delta to 1 or -1, the deeper in-the-money is the option.
The delta of an option’s portfolio is the weighted average of the deltas of all options in the portfolio.
Delta is also known as a hedge ratio. If a trader knows the delta of the option, he can hedge his position by buying or shorting the number of underlying assets multiplied by delta.
Gamma
Gamma (Γ) is a measure of the delta’s change relative to the changes in the price of the underlying asset. If the price of the underlying asset increases by $1, the option’s delta will change by the gamma amount. The main application of gamma is the assessment of the option’s delta.
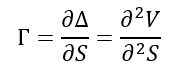
Long options have a positive gamma. An option has a maximum gamma when it is at-the-money (options strike price equals the price of the underlying asset). However, gamma decreases when an option is deep-in-the-money or out-the-money.
Vega
Vega (ν) is an option Greek that measures the sensitivity of an option price relative to the volatility of the underlying asset. If the volatility of the underlying asset increases by 1%, the option price will change by the vega amount.

Where:
- ∂ – the first derivative
- V – the option’s price (theoretical value)
- σ – the volatility of the underlying asset
The Vega is expressed as a monetary amount rather than as a decimal number. An increase in vega generally corresponds to an increase in the option value (both calls and puts).
Theta
Theta (θ) is a measure of the sensitivity of the option price relative to the option’s time to maturity. If the option’s time to maturity decreases by one day, the option’s price will change by the theta amount. The Theta option Greek is also referred to as time decay.
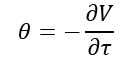
Where:
- ∂ – the first derivative
- V – the option’s price (theoretical value)
- τ – the option’s time to maturity
In most cases, theta is negative for options. However, it may be positive for some European options. Theta shows the most negative amount when the option is at-the-money.
Rho
Rho (ρ) measures the sensitivity of the option price relative to interest rates. If a benchmark interest rate increases by 1%, the option price will change by the rho amount. The rho is considered the least significant among other option Greeks because option prices are generally less sensitive to interest rate changes than to changes in other parameters.
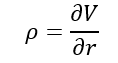
Where:
- ∂ – the first derivative
- V – the option’s price (theoretical value)
- r – interest rate
Generally, call options have a positive rho, while the rho for put options is negative.
In addition to Delta, Gamma, Vega, Theta, and Rho, there are other important Greeks that traders should be aware of. These Greeks include Kappa, which measures the sensitivity of an option's price to skewness; Omega, which measures the sensitivity of an option's price to kurtosis; Lambda, which measures the sensitivity of an option's price to jump risk; and Sigma, which measures the sensitivity of an option's price to the volatility risk premium.
By understanding these Greeks, traders can make more informed decisions when trading options.
Learn Option series next reads:



